বিগত বছরের গণিত অলিম্পিয়াডে আসা কিছু প্রশ্নের সমাধান [পর্বঃ০২]

প্রশ্নঃ

abc0ac একটি ছয় অঙ্কের পূর্ণবর্গ সংখ্যা, যা ৫ ও ১১ দ্বারা বিভাজ্য। সংখ্যাটির সম্ভাব্য সকল মানের যোগফল কত?

 

সমাধানঃ

যেহেতু সংখ্যাটি ৫ দ্বারা বিভাজ্য, সুতরাং সংখ্যাটির একক স্থানীয় অঙ্ক ০ নাহলে ৫ হবে।

যদি সংখ্যাটির একক স্থানীয় অঙ্ক তথা c=0 হয়, তাহলে তৃতীয় অঙ্কটিও 0 হবে। [যেহেতু তৃতীয় অঙ্কটিও c।] অর্থাৎ, অঙ্কটি হবে-

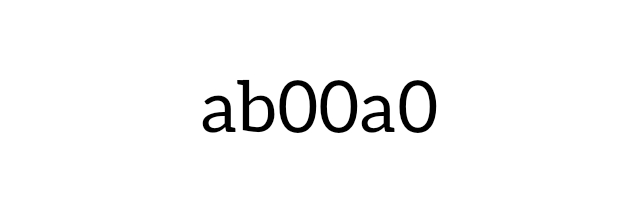
এখন, যেহেতু অঙ্কটি ১১ দিয়েও বিভাজ্য, সুতরাং সংখ্যাটির জোড় স্থানীয় ও বিজোড় স্থানীয় অঙ্কগুলোর সমষ্টির বিয়োগফল হয় ০ হবে, নাহয় ১১ দ্বারা বিভাজ্য হবে।

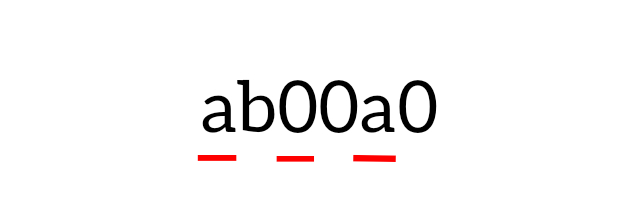
তাহলে, বিজোড় স্থানীয় অঙ্কগুলোর যোগফল

= a+0+a     = 2a

 

আবার,

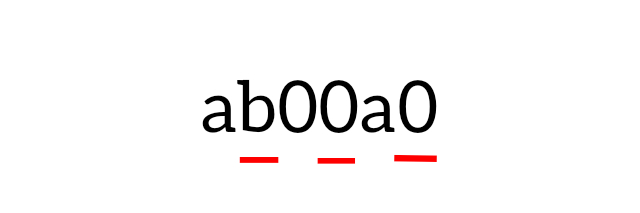
জোড় স্থানীয় অঙ্কগুলোর যোগফল

= b+0+0     = b

∴ বিয়োগফল=2a-b

সুতরাং, 2a-b এর মান হয় 0 হবে, নাহয় 11 দ্বারা বিভাজ্য হবে।

ধরি, 2a-b, 11 দ্বারা বিভাজ্য।

এখানে, a-এর মান 1-9 পর্যন্ত হতে পারবে।

তাহলে 2a-র মান হবে 2,4,6,…,18

যেহেতু 2a-b এর মান 11-এর গুণিতক হবে, সেহেতু 2a-এর মান অবশ্যই 11-র চেয়ে বড় হতে হবে। 2a-র মান যেহেতু সর্বোচ্চ 18 হতে পারবে, তাহলে 2a-b এর মান 11 বাদে 11-র অন্য কোনো গুণিতক (22, 33, 44,…) হতে পারবে না। সেক্ষেত্রে 2a-b এর মান শুধুমাত্র 11 হওয়া সম্ভব।

তাহলে 2a-র মান 11-র থেকে বড় হলে a-র সম্ভাব্য মান হবে 6, 7, 8, 9।

এখন,

a=6 হলে, 2a=12

∴ b=12-11

=1

তাহলে সংখ্যাটি হবে 610060

কিন্তু, সংখ্যাটিকে পূর্ণবর্গ হতে হবে।

∴ √610060 = 781.063377….

অর্থাৎ, এটি পূর্ণবর্গ নয়। তাই এটি গ্রহণযোগ্য নয়।

 

আবার, a=7 হলে, 2a=14

∴ b=14-11

=3

সুতরাং, সংখ্যাটি 730070

√730070 = 854.441338….

এটিও তাহলে গ্রহণযোগ্য নয়।

 

a=8 হলে, 2a=16

∴ b= 16-11

= 5

সুতরাং, সংখ্যাটি 850080

√850080 = 921.997830….

তাহলে, 850080 গ্রহণযোগ্য নয়।

 

a=9 হলে, 2a=18

∴ b= 18-11

=7

সুতরাং, সংখ্যাটি 970090

√970090 = 984.931469….

তাহলে, 970090-ও গ্রহণযোগ্য নয়।

 

যেহেতু 2a-b 11 দ্বারা বিভাজ্য নয়, তাহলে 2a-b=0 হতে পারে।

তাহলে, 2a-b=0

বা, 2a=b

∴ a=b⁄2

 

এক্ষেত্রে b-এর মান অবশ্যই জোড় সংখ্যা হতে হবে। নতুবা, a-এর মান ভগ্নাংশ আসবে।

 

b=2 হলে, a=2⁄2=1

তাহলে সংখ্যাটি 120010

√120010=346.424595….

∴ 120010 গ্রহণযোগ্য নয়।

 

b=4 হলে, a=4⁄2=2

তাহলে সংখ্যাটি 240020

√240020=489.918360….

∴ 240020 গ্রহণযোগ্য নয়।

 

b=6 হলে, a=6⁄2=3

তাহলে সংখ্যাটি 360030

√360030=600.024999….

∴ 360030 গ্রহণযোগ্য নয়।

 

b=8 হলে, a=8⁄2=4

তাহলে সংখ্যাটি 480040

√480040=692.849189….

∴ 480040 গ্রহণযোগ্য নয়।

 

সুতরাং, c=0 হওয়া সম্ভব নয়।

তাহলে, c=5 হলে, সংখ্যাটি হবে-

যেহেতু অঙ্কটি ১১ দিয়েও বিভাজ্য, সুতরাং সংখ্যাটির জোড় স্থানীয় ও বিজোড় স্থানীয় অঙ্কগুলোর সমষ্টির বিয়োগফল হয় ০ হবে, নাহয় ১১ দ্বারা বিভাজ্য হবে।

বিজোড় স্থানীয় অঙ্কগুলোর যোগফল

= a+5+a

= 2a+5

আবার, জোড় স্থানীয় অঙ্কগুলোর যোগফল

= b+0+5

= b+5

∴ বিয়োগফল=(2a+5) – (b+5)

=2a+5-b-5

=2a-b

ধরি,

2a-b এর মান 11 দ্বারা বিভাজ্য।

সেক্ষেত্রে, a এর সম্ভাব্য মান হবে 6, 7, 8, 9

 

এখন,

a=6 হলে, 2a=12

∴ b=12-11

=1

তাহলে সংখ্যাটি হবে 615065

∴ √615065 = 784.260798….

অর্থাৎ, এটি পূর্ণবর্গ নয়। তাই এটি গ্রহণযোগ্য নয়।

 

আবার, a=7 হলে, 2a=14

∴ b=14-11

=3

সুতরাং, সংখ্যাটি 735075

√735075 = 857.365149….

এটিও তাহলে গ্রহণযোগ্য নয়।

 

a=8 হলে, 2a=16

∴ b= 16-11

= 5

সুতরাং, সংখ্যাটি 855085

√855085 = 924=708062….

তাহলে, 855085 গ্রহণযোগ্য নয়।

 

a=9 হলে, 2a=18

∴ b= 18-11

=7

সুতরাং, সংখ্যাটি 975095

√975095 = 987.468986….

তাহলে, 975095-ও গ্রহণযোগ্য নয়।

 

যেহেতু 2a-b 11 দ্বারা বিভাজ্য নয়, তাহলে 2a-b=0 হতে পারে।

 

তাহলে, 2a-b=0

বা, 2a=b

∴ a=b⁄2

 

এক্ষেত্রে b-এর মান অবশ্যই জোড় সংখ্যা হতে হবে। নতুবা, a-এর মান ভগ্নাংশ আসবে।

b=2 হলে, a=2⁄2=1

তাহলে সংখ্যাটি 125015

√125015=353.574603….

∴ 125015 গ্রহণযোগ্য নয়।

 

b=4 হলে, a=4⁄2=2

তাহলে সংখ্যাটি 245025

√245025=495

∴ 245025 গ্রহণযোগ্য।

 

b=6 হলে, a=6⁄2=3

তাহলে সংখ্যাটি 365035

√365035=604.181264….

∴ 365035 গ্রহণযোগ্য নয়।

 

b=8 হলে, a=8⁄2=4

তাহলে সংখ্যাটি 485045

√485045=696.451721….

∴ 485045 গ্রহণযোগ্য নয়।

 

সুতরাং, abc0ac সংখ্যাটির কেবলমাত্র একটি মান পাওয়া সম্ভব, তা হচ্ছে 245025।

তাই abc0ac-এর সম্ভাব্য সকল মানের যোগফল 245025।

Ans: 245025.