বিগত বছরের গণিত অলিম্পিয়াডে আসা কিছু প্রশ্নের সমাধান [পর্বঃ০১]

আসসালামু আলাইকুম। ছোট-বড় সকলকে জানাই শুভকামনা। বাংলাদেশে অনেক বছর ধরেই একটি জনপ্রিয় প্রতিযোগিতা “গণিত অলিম্পিয়াড” অনুষ্ঠিত হয়ে আসছে। এবছরও অনলাইনে বাছাই পর্ব শুরু হলেও কারিগরি ত্রুটির কারণে পরবর্তীতে তা স্থগিত করা হয়। যাই হোক, আসল কথা হচ্ছে বিগত বছরে আসা প্রশ্নগুলোর তেমন কোনো সমাধান পাওয়া যায় না। তাই আমার একটু ক্ষুদ্র চেষ্টা, যদিও আমি গণিতে বিদ্যার জাহাজ নই! আরেকটা কথা, গণিত অলিম্পিয়াডের প্রশ্নগুলো হয় সৃজনশীলের মতো। অর্থাৎ, পুঁথিগত বিদ্যা এগুলো Solve করা সম্ভব নয়। এগুলো এমন প্রশ্ন, যা তোমাকে ভাবতে বাধ্য করবে। আর এগুলো এমন অঙ্ক, যেগুলো শুধু ছোটদের জন্য নয়, চাকরির ক্ষেত্রেও কাজে লাগে। তো আজ থেকে শুরু হলো নতুন ধারাবাহিক। প্রতিটা পর্বে আমি একটা করে প্রশ্নের সমাধান করে দিবো। আজকে একটা জ্যামিতিক সমস্যা দিয়েই শুরু করা যাক। আমি ভাবলাম, প্রথমে একটু সহজ জিনিস করে দিলেই হয়তো ভালো হবে। আচ্ছা চলো, শুরু করা যাক।

নিচের প্রশ্নটা খেয়াল করো- ???

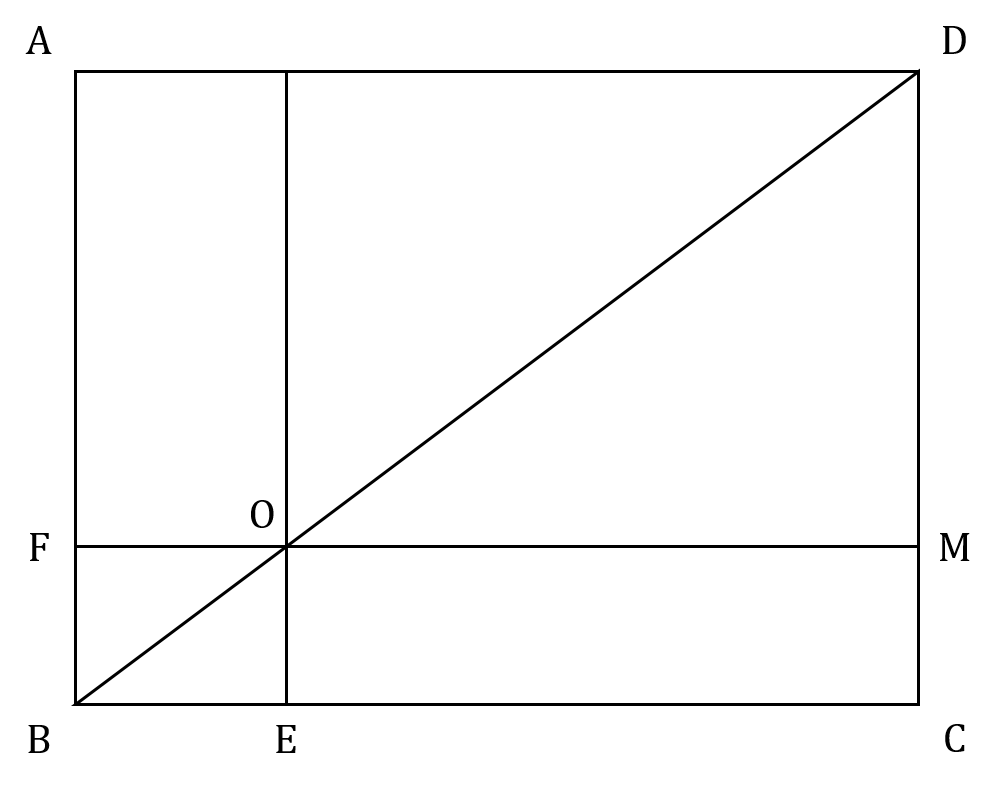
প্রশ্নঃ ABCD একটি আয়তক্ষেত্র। AD=16, BE=4 এবং AB=12। ODM-এর ক্ষেত্রফল কত?

সমাধানঃ

চিত্রটিতে একটি বিন্দুর নামকরণ P করা হলো।

[প্রথমেই বলে রাখি, এই প্রশ্নে একটা ভুল আছে। এখানে অবশ্যই বলতে হতো PE ∥ AB এবং FM ∥ AD। নাহলে এই প্রশ্ন সমাধান করা অসম্ভব। এখানে সেটা নিয়ে করা হলো।]

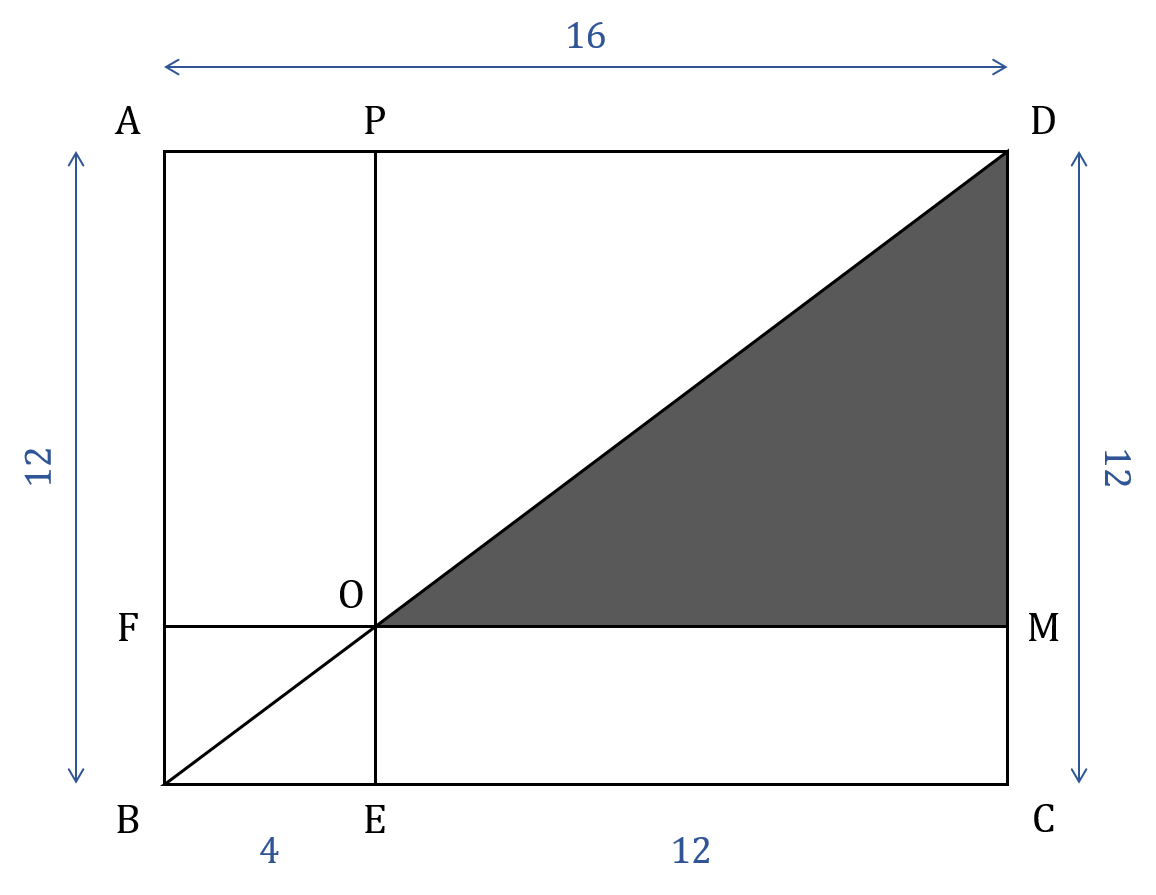
দেওয়া আছে,

ABCD একটি আয়তক্ষেত্র

∴ AB=CD   এবং   AD=BC, AB ∥ CD এবং AD ∥ BC     [আয়তের বিপরীত বাহুগুলো সমান ও সমান্তরাল]

AD=16,   BE=4,   AB=12

সুতরাং, BC=16   এবং   CD=12

আবার, PE ∥ AB  অর্থাৎ, PE ∥ CD  [∵ AB ∥ CD]

∴ PE=AB=CD=12 [PE, AB ও CD-এর সমান্তরাল ছেদক]

অনুরূপভাবে লেখা যায়,

FM=AD=BC=16

আবার,

যেহেতু, ABCD একটি আয়তক্ষেত্র

∴ ∠A=∠B=∠C=∠D=90°

PE ∥ AB হওয়ায়,

∠B=∠E=∠C

AB এবং CD, BC-এর উপর লম্ব।

∴PE ⊥ BC

অনুরূপভাবে লেখা যায়, FM⊥CD

সুতরাং, ∆ODM ও ∆BCD-এর যথাক্রমে ∠M ও ∠C কোণ সমকোণ।

∴ ∆ODM ও ∆BCD সমকোণী ত্রিভুজ

এখন,

যেহেতু, AD=FM=BC, AD ∥ FM ∥ BC এবং PE ⊥ AD, FM, BC;

∴ AP=OF=BE

এবং PD=OM=EC

অনুরূপভাবে লেখা যায়,

AF=OP=MD

এবং BF=OE=CM

এখন,

BC=16

বা, BE+EC=16

বা, 4+EC=16

বা, EC=16-4

∴ EC=12

সুতরাং, OM=PD=12

∆ODM-এর ভূমি=OM=12

∆BCD-এর ভূমি=BC=16 এবং লম্ব=CD=12

∆ODM ও BCD সমকোণী ত্রিভুজের মধ্যে-

∠OMD=∠BCD    [প্রত্যেকে সমকোণ]

∠ODM=∠BDC    [∠ODM, BDC-এর অংশ]

সুতরাং, ∆ODM ও ∆BCD পরস্পর সদৃশ।

∴ MD⁄OM = CD⁄BC

বা, MD⁄12 = 12⁄16

বা, 16MD = 12×12

বা, MD = 12×12 ⁄16

∴ MD = 9

∴ ∆ODM-এর ক্ষেত্রফল = 1⁄2 × ভূমি × উচ্চতা

= 1⁄2 × OM × MD বর্গ একক

= 1⁄2 × 12 × 9 বর্গ একক

=54 বর্গ একক

Ans : 54 বর্গ একক।

ধন্যবাদ। সবাই ভালো থাকো, সুস্থ থাকো। আর কোনো জটিল সমস্যা থাকলে Comment করে লিখবে। আমি Solve করে দেওয়ার চেষ্টা করবো। আল্লাহ হাফেজ।